جدول المحتويات
درسنا اليوم عن التكاملات غير المحدودة وأهم القواعد والطرق المختلفة لايجاد التكامل. مع أمثلة كثيرة محلولة عن التكامل غير المحدود. بالإضافة إلى إضاءة بسيطة عن التكامل بالتعويض.
إن كنت تبحث عن المزيد من المسائل للتدريب يمكنك قراءة مقال مسائل في التكامل غير المحدود
ما هو التكامل
التكامل هو أحد العمليات الأساسية في حساب التفاضل والتكامل، وهو بمثابة العملية العكسية للاشتقاق. يتضمن التكامل إيجاد دالة أصلية لدالة معينة، بحيث يكون اشتقاق الدالة الأصلية هو الدالة المعطاة. في هذا المقال، سنتناول بالتفصيل مفهوم التكامل غير المحدود، والقواعد الأساسية المستخدمة في حله، بالإضافة إلى أمثلة توضيحية.
ما هو التكامل غير المحدود؟
التكامل غير المحدود، والذي يُرمز إليه بالرمز ∫، هو عملية إيجاد جميع الدوال التي يكون مشتقها هو الدالة المعطاة. بعبارة أخرى، إذا كانت f(x) هي دالة، فإن التكامل غير المحدود لها هو F(x) + C، حيث F '(x) = f(x) و C هو ثابت تكامل عشوائي.
مثال: إذا كانت f(x) = 2x، فإن تكاملها غير المحدود هو F(x) = x² + C، حيث مشتق x² هي 2x.
لماذا نضيف ثابت التكامل؟
نضيف ثابت التكامل C إلى نتيجة التكامل لأن هناك عدد لا نهائي من الدوال التي يكون مشتقها هو نفس الدالة المعطاة. فمثلاً، كل من الدوال x²، x² + 1، x² - 3، .الخ، يكون مشتقها هو 2x. لذلك، فإن إضافة ثابت التكامل يمثل جميع الحلول الممكنة.
القواعد الأساسية للتكامل غير المحدود

هناك العديد من القواعد الأساسية التي تستخدم لحساب التكاملات غير المحددة، ومن أهمها:
- تكامل التابع الثابت:
∫ a dx = ax + Cحيث a هو ثابت عددي.
حالة خاصة: تكامل الـ 1 هو x + C - تكامل تابع القوة:
∫ xⁿ dx = (xⁿ⁺¹)/(n+1) + Cحيث n ≠ -1. - تكامل التابع الأسي:
∫ aˣ dx = aˣ/ln(a) + C: a>0,a≠1
تكامل التابع الأسي النيبري∫ eˣ dx = eˣ + C - تكامل التابع الكسري:
∫ 1/x dx =ln |x| + C - تكامل الدالة المثلثية:
تكامل∫ sin(x) dx = -cos(x) + C
تكامل∫ cos(x) dx = sin(x) + C
تكامل∫ sec2(x) dx = tan(x) + C
تكامل∫ csc2(x) dx = -cot(x) + C
تكامل∫ sec x(tan x) dx = sec(x) + C
تكامل∫ csc x(cot x) dx = -csc(x) + C - تكامل التوابع الزائدية والمثلثية المعكوسة: التوابع الزائدية هي التوابع المعرفة بالقطع الزائد بدل الدائرة.
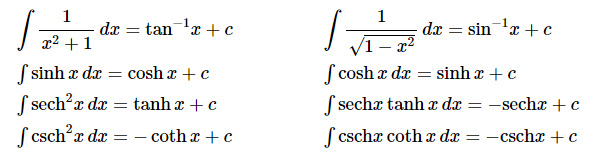
خواص التكامل غير المحدود
- تكامل مجموع تابعين:
∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx - الثوابت:
∫ af(x) dx = a∫ f(x) dx - خاصية الخطية:
∫ [af(x) + bg(x)] dx = a∫ f(x) dx + b∫ g(x) dxحيث a و b ثوابت عددية.
خواص التكامل المحدود
للتكامل غير المحدود خواص كثيرة سنذكر 5 منها:
- عند تبديل حدود التكامل يجب عكس الاشارة.
- يمكن إخراج العدد الثابت خارج حدود التكامل.
- تكامل مجموع/طرح تابعين = تكامل التابع الأول ± تكامل التابع الثاني
- إمكانية تجزية التكامل.
- الخاصية الخامسة هي مبرهنة.
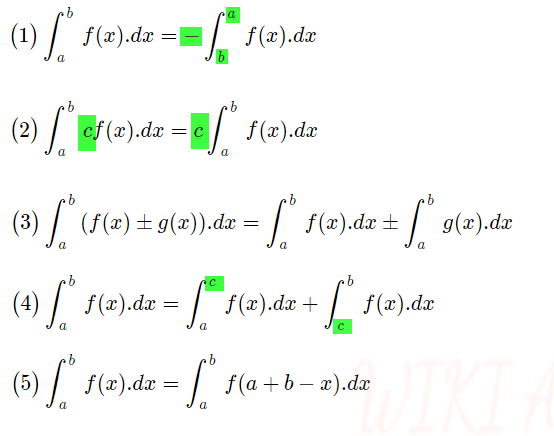
أمثلة على التكامل غير المحدود
إليكم مجموعة من الأمثلة والتمارين التطبيقية التي تساعد على فهم التكامل غير المحدود من خلال تطبيق القواعد السابقة في الحل.
مثال 1: أوجد تكامل الدالة f(x) = 3x² + 2x - 1.
الحل: باستخدام قاعدة تابع القوة : ∫ xⁿ dx = (xⁿ⁺¹)/(n+1) + C
∫ (3x² + 2x - 1) dx = 3∫ x² dx + 2∫ x dx - ∫ dx= x³ + x² - x + C
مثال 2: أوجد تكامل الدالة f(x) = eˣ + sin(x).
الحل: لحساب تكامل الدالة f(x) = eˣ + sin(x) نقوم بتطبيق قواعد التكامل الأساسية.
∫ (eˣ + sin(x)) dx= ∫ eˣ dx + ∫ sin(x) dx= eˣ - cos(x) + C
بالتالي، تكامل الدالة f(x) = eˣ + sin(x) يساوي eˣ - cos(x) + C حيث C يمثل الثابت التكاملي.
تمارين حول التكامل غير المحدود
فيما يلي مسائل بسيطة حول التكامل غير المحدود. يمكنك الاطلاع على مقال مسائل التكامل غير المحدود لمزيد من الأمثلة والتمرينا.
أوجد التكاملات التالية:
-
∫(2x + 3) dx ∫(4cos(x) - 2sin(x)) dx∫(x2 - 5x + 1) dx-
∫(2ex - 3x) dx ∫(1/x + x3) dx
يمكنك الآن تطبيق القواعد السابقة على هذه الأسئلة ومراجعة الحل كاملا هنا:
1. حساب التكامل ∫(2x + 3)dx باستخدام قاعدة القوة:
∫(2x + 3) dx = x2 + 3x + C
2. حساب التكامل ∫(4cos(x) - 2sin(x))dx:
∫(4cos(x) - 2sin(x)) dx = 4sin(x) + 2cos(x) + C
3. حساب التكامل ∫(x2 - 5x + 1)dx:
∫(x2 - 5x + 1) dx = (x3)/3 - (5x2)/2 + x + C
4. حساب التكامل ∫(2ex - 3x)dx:
∫(2ex - 3x) dx = 2ex - (3x2)/2 + C
5. حساب التكامل ∫(1/x + x3)dx:
∫(1/x + x3) dx = ln|x| + (x4)/4 + C
التكامل بالتعويض
التكامل بالتعويض هو أسلوب يستخدم لإيجاد تكامل الدوال المعقدة. يتم ذلك عن طريق استبدال جزء من الدالة بمتغير جديد، وبالتالي تبسيط التكامل.
مثال 1: أوجد تكامل التابع f(x) = x * ex².
الحل: لحساب تكامل الدالة f(x) = x * e^(x²)، سنستخدم قاعدة تكامل الدوال المُشتقة. يتم الحساب كالتالي: نفرض u = x², وبالتالي du = 2x dx.
باستخدام هذه التبديلات، يمكننا استبدال x dx بـ (1/2)du
إذن،
∫ x * ex² dx = (1/2) ∫ eu du= (1/2) eu + C = (1/2) ex² + C.
مثال 2 عن التكامل بالتعويض: احسب التكامل التالي: ∫(2x * sin(x²)) dx
نقوم بتطبيق بعض التغيرات البسيطة للتابع. نفرض u = x² وبالتالي يكون du = 2x dx. نستبدل 2x dx بـ du، ونقوم بتبسيط الدالة إلى:
∫sin(u) du = -cos(u) + C =-cos(x²) + C
في الختام
التكامل غير المحدود هو أداة أساسية في حساب التفاضل والتكامل، ويستخدم لحل العديد من المسائل في الفيزياء والهندسة وغيرها من المجالات. من خلال فهم القواعد الأساسية للتكامل والتعرف على أساليب مثل التكامل بالتعويض، يمكن للطالب حل مجموعة واسعة من التكاملات.
ملاحظات:
- هناك العديد من الطرق الأخرى لحساب التكاملات، مثل التكامل بالتجزئة والتكامل بالكسور الجزئية.
- يمكن استخدام الحاسبات العلمية والبرامج المتخصصة لحساب التكاملات المعقدة.
هل لديك أي أسئلة أخرى حول التكامل غير المحدود؟ يمكنك ذكرها في التعليقات لنحاول الإجابة عنها سوية.